Valuing annuities #

Finding the present value of a series of equal payments \(=\) “annuities”:

• So far we have considered the calculation of the present value and the accumulated value of single cash flows.
• It is quite common in practice for the same cash flows to be repeated many times. For example,
  • a new home owner may repay the bank $500 every fortnight over a 25 year period
  • or a life insurance company might pay a retiree $1,500 every month for the rest of the person’s life.
• In order to value (that is, to find the present value of) a series of payments, we could find the present value of each individual payment in the series of payments and sum the resulting series.
• This approach will very quickly become tedious for long series of cash flows. We therefore develop formulae for finding the present value of streams of equal payments.

Annuity in arrears – Annuity-Immediate #

Definition #

Consider the figure below which contains \(n\) years. Consider the case where a payment of $1 is made at the end of each of the \(n\) years marked in the diagram. Suppose we want to find the present value of these payments – that is, their value at time 0.

We perform this calculation very often and so we give a symbol for the present value result. Define \begin{align} a_{\angl{n}}=v+v^{2}+\ldots +v^{n} \end{align} This type of annuity is called an annuity in arrears because
the payments are made at the end of each year.

Example 1 #

1. Write down an expression in terms \(v\) for \((1+i)a_{\angl{n}}.\)
2. Use part (1) and the definition of \(a_{\angl{n}}\) to derive an expression for \(ia_{\angl{n}}.\) Hence show that \begin{align} a_{\angl{n}}=\frac{1-v^{n}}{i}. \end{align}
3. If we rearrange our result from (2), we get $$1=ia_{\angl{n}}+v^{n}. $$ Interpret this expression in terms of a loan of $1 and the associated repayments.

Solution to Part 1 #

We have $$ \textcolor{red}{(1+i)a_{\angl{n}}=1+v+v^2+\ldots+v^{n-1} }$$

Solution to Part 2 #

Subtract the definition from the result in (1) to get $$\textcolor{red}{ia_{\angl{n}}=1-v^n} $$ Make \(a_{\angl{n}}\) the subject and the result is proved.

Solution to Part 3 #

We need to interpret $$1=ia_{\angl{n}}+v^{n}$$ For a loan of $1 today, we can repay interest (only) on the loan at the end of each year for \(n\) years and then repay the amount borrowed ($1) in \(n\) years’ time.

The present value of the borrowings ($1) must equal the present value of the interest repayments \((i\,a_{\angl{n}})\) plus the present value of the repayment of principal, \(v^{n}\), i.e. $$ 1=ia_{\angl{n}}+v^{n} \quad \text{ and hence } \quad a_{\angl{n}}=\frac{1-v^{n}}{i}.$$

Part 3: A concrete example #

• Take \(n=10, i=5\%\). That is to say, $$100=5 a_{\angl{10}}+100 v^{10} $$
• Suppose I lend you $100 and charge you interest at 5% per annum effective. This means your debt in one year’s time will be $105.
• Suppose you repay $5 at the end of 1 year – you have repaid the interest only, and still owe me $100.
• At the end of the second year you again repay $5 – your debt is still $100.
• Suppose this pattern continues for 10 years – each year you pay $5 at the year end, and at the end of the 10th year you repay the $100.
• Your repayments can be represented as a 10 year annuity in arrears of amount 5, and a payment of 100 at time 10 years.
• As my loan has been repaid, the present value of my outgo equals that of my income, i.e. $$100=5a_{\angl{10}}+100v^{10}. $$

Part 2: Alternative derivation #

How else could you derive the result in (2)?

By using the sum of a geometric progression with \(n\) terms, first term \(v\) and common ratio equal to \(v\), we get \begin{eqnarray*} a_{\angl{n}} &=&v+v^{2}+\ldots +v^{n} \\ &=&v (1+v^2+\ldots+v^{n-1}) \\ &=&v\frac{1-v^{n}}{1-v} \\ &=& \frac{1-v^{n}}{(1/v)-1}. \end{eqnarray*} As $$1/v=1+i, $$ we get $$a_{\angl{n}}=\frac{1-v^{n}}{i}. $$

Annuity in advance – Annuity-Due #

Definition #

• The annuity we considered above is called an annuity in arrears since the payments are made at the end of each of the \(n\) years.
• Suppose instead that the payments are made at the start of each of the \(n\) years.
• The annuity is then called an annuity in advance, or annuity-due.
• Mark the payments and the valuation date on the diagram below for an \(n\) year annuity in advance.
• The present value of an annuity in advance is written as \(\ddot{a}_{\angl{n}}\) and is pronounced “a due \(n\).”

Example 2 #

1. Write down a sum in terms of \(v\) for \(\ddot{a}_{\angl{n}}\).
2. Explain in words why $$\ddot{a}_{\angl{n}}=(1+i)a_{\angl{n}}.$$
3. Show that $$\ddot{a}_{\angl{n}}=1+a_{\angl{n-1}}.$$

Solution to Part 1 #

We have $$\ddot{a}_{\angl{n}}=1+v+v^2+\ldots+v^{n-1}.$$

Solution to Part 2 #

The number of payments and the valuation interest rates are the same. The only difference is that payments occur one year earlier in \(\ddot{a}_{\angl{n}}\) as compared with \(a_{\angl{n}}\), which explains why it is worth more, by a factor or \((1+i)\).

Solution to Part 3 #

Using our definition for \(a_{\angl{n}}\), we can write $$a_{\angl{n-1}}=v+v^{2}+…+v^{n-1}. $$ This clearly includes every term in the summation for \(\ddot{a}_{\angl{n}}\) except the initial payment of 1. Therefore $$\ddot{a}_{\angl{n}}=1+a_{\angl{n-1}}.$$

Example 3 #

1. Find the PV of 20 annual payments of $1,000 at 6% per annum effective with the first payment due in 12 months’ time.
2. Find the PV of 15 annual payments of $700 at 5% per annum effective with the first payment due immediately.

Solutions:

1. $$1,000a_{\angl{20}}=1,000\frac{1-1.06^{-20}}{0.06}=11,469.92.$$
2. $$700\ddot{a}_{\angl{15}}=700(1.05)a_{\angl{15}}=7,629.05.$$

Some reasonableness checks for annuities #

Quite often in actuarial work, we are involved with very complex calculations. It is useful to be able to place a rough check (a reasonableness check) on our work at the end. This can be a useful way to remove any careless errors that we may have been made during the course of our work.

First check #

First, (assuming \(i\geq 0\)) \begin{eqnarray*} a_{\angl{n}} &=&v+v^{2}+v^{3}+\ldots +v^{n} \\ &\leq & 1+1+1+\ldots +1=n. \end{eqnarray*} Thus, the value of \(a_{\angl{n}}\) cannot exceed \(n\).

Second check #

Second, (assuming \(i>0\)) $$a_{\angl{n}}=\frac{1-v^{n}}{i}\rightarrow \frac{1}{i}\text{ as }n\rightarrow \infty $$ Thus, **the value of \(a_{\angl{n}}\) cannot exceed \(1/i\)**.

Third check #

Third, consider the amounts and the timing of the payments:

• Each of the \(n\) payments is of amount 1, so the total amount is \(n\).
• The payment times are \(1,2,\ldots ,n\), so the average payment time is $$\frac{1}{n}\left( 1+2+\ldots +n\right) =\frac{n(n+1)}{2n}=\frac{n+1}{2}.$$ Hence, an approximation of \(a_{\angl{n}}\) is $$a_{\angl{n}}\approx nv^{\frac{n+1}{2}}.$$

For example, compare at 6%: $$a_{\angl{20}}=\frac{1-1.06^{-20}}{0.06}=11.4699, $$ while $$20\times 1.06^{-10.5}=10.85. $$

Example 4 #

1. Calculate the PV of a series of payments of $100 at the end of each of the next 20 years at 9% per annum effective.
2. Calculate the PV of a series of payments of $100 at the beginning of each of the next 15 years at 8% per annum convertible quarterly.
3. Apply a reasonableness check to your answer to Part (2).

Solutions:

1. The PV is $$100a_{\angl{20}}=100\frac{1-1.09^{-20}}{0.09}=912.85$$
2. The PV is $$100\ddot{a}_{\angl{15}}=100(1+i)\frac{1-(1+i)^{-15}}{i}=912.90,$$ where \(1+i=1.02^4\).
3. The PV is approximately $$100\times 15v^{7}=1,500\times 1.02^{-28}=$861. $$ ($\frac{1}{15}\times\frac{1}{2}\times 14\times 15=7$)

Perpetuities #

Definition #

• In fact, this infinite term annuity seen before is called a perpetuity, and is written \begin{eqnarray*} a_{\angl{\infty}i}&=& v+ v^2+ v^3 + \ldots\\ &=& v (1 + v+ v^2+ v^3 + \ldots) \\ &=& \frac{v}{1-v} \\ &=& \frac{1}{i} \end{eqnarray*}
• This can also be used as a building block to derive annuity formulas.

Example 5 #

Derive the formula for an annuity-immediate $$a_{\angl{n}}=\frac{1-v^{n}}{i}$$ using perpetuity $$a_{\angl{\infty}i}=\frac{1}{i}.$$

Solution:

• Consider the difference between two infinite series of payment of 1, one starting now with present value $$a_{\angl{\infty}i}=\frac{1}{i},$$ and one starting in \(n\) years with present value $$ v^n a_{\angl{\infty}i}=v^n \frac{1}{i}.$$
• The difference in cash flows corresponds exactly to that of an annuity-immediate over \(n\) years, with present value $$\frac{1}{i}-v^n \frac{1}{i} =\frac{1-v^n}{i}= a_{\angl{n}},$$ as required.

Deferred annuities #

Definition #

We now develop formulae for annuities where the first payment is delayed by \(m\) years. We again consider the case where \(n\) payments are made in total.

Consider first the annuity in arrears. In the non-deferred case, the first payment is made at the end of the first year, that is, at time 1. In the deferred annuity, the first payment is therefore made at time \(m+1\), that is, at the end of the \((m+1)\)st year.

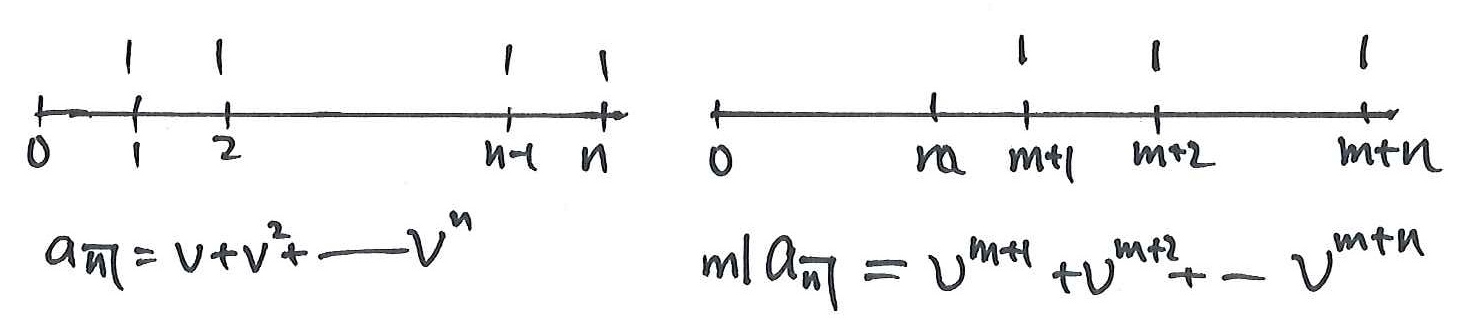
The notation used for the present value of an \(m\) year deferred, \(n\) year annuity with payments in arrears is \(_{m|}a_{\angl{n}}\).

Example 6 #

1. Write down an expression for \(_{m|}a_{\angl{n}}\) in terms of \(v\).
2. Write an expression for \(_{m|}a_{\angl{n}}\) in terms of \(v\), \(m\) and \(a_{\angl{n}}.\)

Solutions:

1. $$_{m|}a_{\angl{n}}=v^{m+1}+v^{m+2}+\ldots+v^{m+n}$$
2. From above, the expression for \(_{m|}a_{\angl{n}}\) involves \(m\) years further discounting for each term than is required under \(a_{\angl{n}}.\) Therefore, we have $$_{m|}a_{\angl{n}}=v^m(v+v^2+\ldots+v^n)=v^ma_{\angl{n}}.$$

Formula \(_{m|}a_{\angl{n}}=a_{\angl{m+n}}-a_{\angl{m}}\) #

Proof of \(_{m|}a_{\angl{n}}=a_{\angl{m+n}}-a_{\angl{m}}\) #

Using the result in part (2) of Example 6 above, we have \begin{eqnarray*} _{m|}a_{\angl{n}} &=&v^{m}a_{\angl{n}} = v^{m}\frac{1-v^{n}}{i} = \frac{v^{m}-v^{m+n}}{i} \\ && \\ &=& \frac{1-v^{m+n}-(1-v^{m})}{i} = a_{\angl{m+n}}-a_{\angl{m}}. \end{eqnarray*}

Interpretation #

$$_{m|}a_{\angl{n}}=a_{\angl{m+n}}-a_{\angl{m}}\Longleftrightarrow a_{\angl{m+n}}=a_{\angl{m}}+_{m|}a_{\angl{n}}$$

Example 7 #

Find the PV of a series of 15 payments of $1 at yearly intervals beginning 11 years from now. Use an interest rate of 7% per annum effective.

• Method One: The PV is \begin{eqnarray*} _{10|}a_{\angl{15}} &=&v^{10}\ \frac{1-v^{15}}{i} = 1.07^{-10}\ \frac{1-1.07^{-15}}{0.07} = 4.63. \end{eqnarray*}
• Method Two: The PV is \begin{eqnarray*} a_{\angl{25}}-a_{\angl{10}} &=&\frac{1-1.07^{-25}}{0.07}-\frac{1-1.07^{-10}}{0.07}\\ =4.63. \end{eqnarray*}
• Rough Check: PV \(\approx 15v^{18}=4.44.\)

Annuities payable in \(m\) partial payments #

Annuities payable \(m\)-thly #

• We have already discussed annuities where payments are made for \(n\) years with one payment of $1 each year.
• We now break up that single payment of $1 into \(m\) payments each of $ \(1/m\)
• Consider the following timeline and mark on the payments for a \(n\) year annuity with payments made \(m\) times per year, where each payment is made at the end of \(m\)-th of a year.

\(m\)-thly annuity in arrears / annuity-immediate #

The notation used for an \(m\)-thly annuity with payments at the end of each \(m\)-th of a year is $$a_{\angl{n}}^{(m)}.$$ The derivation of a formula for this annuity is as follows: $$a_{\angl{n}}^{(m)}=\frac{1}{m}\left( v^{1/m}+v^{2/m}+\ldots +v^{nm/m}\right) $$ and $$(1+i)^{1/m}a_{\angl{n}}^{(m)}=\frac{1}{m}\left( 1+v^{1/m}+\ldots+v^{(nm-1)/m}\right)$$

Subtracting the first identity from the second gives $$a_{\angl{n}}^{(m)}\left( (1+i)^{1/m}-1\right) =\frac{1}{m}\left( 1-v^{nm/m}\right) $$ or, equivalently,$$a_{\angl{n}}^{(m)}=\frac{1-v^{n}}{m\left( (1+i)^{1/m}-1\right) }=\frac{1-v^{n}}{i^{(m)}}$$`

\(m\)-thly annuity-due #

The notation used for an \(m\)-thly annuity with payments at the beginning of each \(m\)-th of a year is $$\ddot a_{\angl{n}}^{(m)}.$$ The derivation of a formula for this annuity is as follows: \begin{eqnarray*} \ddot a_{\angl{n}}^{(m)}&=&\frac{1}{m}\left(1+ v^{1/m}+v^{2/m}+\ldots +v^{(nm-1)/m}\right)\\ &=&v^{-1/m}\frac{1}{m}\left(v^{1/m}+v^{2/m}+\ldots +v^{nm/m}\right)\\ &=&(1+i)^{1/m} a_{\angl{n}}^{(m)} \end{eqnarray*}

Examples #

Example 8 #

Find the PV of $100 per annum payable quarterly in arrears for 10 years at 7.5% per annum effective.

Solution:

We have $$100a_{\angl{10}}^{(4)}=100\frac{1-1.075^{-10}}{i^{(4)}}=705.42,$$ where $$i^{(4)}=0.072978.$$

Example 9 #

Find the PV of $100 per annum payable quarterly in arrears for 10 years given interest is 8% per annum convertible quarterly.

Solution: \begin{align*} 1+i &=1.02^4 \\ 100a_{\angl{10}}^{(4)} &= 100\frac{1-v^{10}}{i^{(4)}} \\ &= 100\frac{1-1.02^{-40}}{0.08} \\ &= 683.89 \end{align*}

Alternative derivations #

An alternative expression for \(a_{\angl{n}}^{(m)}\) #

Changing the time unit, \begin{align*} a_{\angl{n}}^{(m)} &= \frac{1-v^{n}}{i^{(m)}}=\frac{1}{m}\frac{1-(v^{1/m})^{nm}}{\frac{i^{(m)}}{m}} \\ &=\frac{1}{m}a_{\angl{nm}\,\,j} \end{align*}

In the above formula,

• The time unit is \(1/m\) of a year;
• \(j=i^{(m)}/m\) is the effective interest rate per time unit;
• \(v^{1/m}=1/(1+j)\) is the discount per time unit ($1/m$ of a year);
• \(1/m\) is the amount of payment per unit of time;
• \(nm\) is the number of payments.

An alternative expression for \(a_{\angl{n}}^{(m)}\) – Using perpetuities #

By analogy, we have $$a_{\angl{\infty}i^{(m)}} = \frac{1}{i^{(m)}}.$$ The result immediately follows.

Accumulated values of annuities #

Definition #

• Consider a superannuation fund into which payments are made during the working life of an individual. These payments will form a regular stream of payments and we are interested in knowing how much these payments will be worth at retirement, when interest is applied to each of the payments.
• We therefore are often interested in calculating the accumulated value of an annuity.
• \(s_{\angl{n}}\) represents the accumulation at time \(n\) of a series of payments of 1 at unit intervals in arrears (i.e. at times \(1,2,\ldots ,n\)). Mark the payments and the valuation date on the timeline below.

Accumulated value of an annuity in arrears #

We derive an expression for \(s_{\angl{n}}\) in a very similar way to how we derived formulae for present values of annuities: $$s_{\angl{n}}=(1+i)^{n-1}+(1+i)^{n-2}+\ldots +(1+i)+1 $$ gives $$(1+i)s_{\angl{n}}=(1+i)^{n}+(1+i)^{n-1}+\ldots +(1+i), $$ and so $$is_{\angl{n}}=(1+i)^{n}-1. $$ Thus, $$s_{\angl{n}}=\frac{(1+i)^{n}-1}{i}. $$

Relationship between \(s_{\angl{n}}\) and \(a_{\angl{n}}\) #

We now derive a relationship between \(s_{\angl{n}}\) and \(a_{\angl{n}}\):

Result: $$s_{\angl{n}}=(1+i)^{n}a_{\angl{n}}. $$

Proof: $$s_{\angl{n}}=\frac{(1+i)^{n}-1}{i}=(1+i)^{n}\frac{1-v^{n}}{i}=(1+i)^{n}a_{\angl{n}}. $$

Accumulated values of an annuity-due #

Suppose now that the \(n\) payments considered above are made at the start of each of the \(n\) years of the annuity. The payments are therefore made in advance.

We aim to find the value of these payments at time \(n\). Mark the payments and valuation date on the diagram below.

Notation: \(\ddot{s}_{\angl{n}}\) represents the accumulation at time \(n\) of a series of payments of 1 at unit intervals in advance (i.e. at times \(0,1,2,\ldots ,n-1\)).

Examples #

Example 10 #

1. Write down an expression in terms of \(i\) and \(n\) for \(\ddot{s}_{\angl{n}}.\)
2. Show that $$\ddot{s}_{\angl{n}}=(1+i)^{n+1}\ a_{\angl{n}}=(1+i)^{n}\ \ddot{a}_{\angl{n}}$$

Solutions:

1. $$\ddot{s}_{\angl{n}}=(1+i)^{n}+(1+i)^{n-1}+\ldots+(1+i)$$
2. \begin{align*} \ddot{s}_{\angl{n}}&=(1+i)s_{\angl{n}}=(1+i)\frac{(1+i)^n-1}{i} \\ &=(1+i)(1+i)^na_{\angl{n}} \\ &=(1+i)^n\,\ddot{a}_{\angl{n}} \end{align*}

Example 11 #

1. Find the PV of a series of 10 payments of $100 at yearly intervals. The first payment is due in 3 months’ time. The interest rate is 8% per annum effective.
2. From first principles, find the accumulated value of the series above at time 12 years.
3. Check that your answers are consistent.

Solutions:

1. The PV is \begin{eqnarray*} &&100\left( v^{\frac{1}{4}}+v^{1\frac{1}{4}}+\ldots +v^{9\frac{1}{4}}\right) \\ &=& 100v^{\frac{1}{4}}\left( 1+v+\ldots +v^{9}\right) \\ &=& 100v^{\frac{1}{4}}\,\ddot{a}_{\angl{10}} \\ &=& 100(1.08^{-0.25})\frac{1-1.08^{-10}}{0.08}1.08 \\ &=& \$710.88. \end{eqnarray*}

1. The accumulated value is \begin{eqnarray*} &&100\left( (1+i)^{11\frac{3}{4}}+(1+i)^{10\frac{3}{4}}+\ldots +(1+i)^{2\frac{3}{4}}\right) \\ &=& 100(1+i)^{2\frac{3}{4}}\left( (1+i)^{9}+(1+i)^{8}+\ldots +1\right) \\ &=& 100(1+i)^{2\frac{3}{4}}\ s_{\angl{10}} \\ &=& 100(1.08)^{2\frac{3}{4}}\ \frac{1.08^{10}-1}{0.08} \\ &=& \$1,790.11. \end{eqnarray*}
2. The valuation dates are 12 years apart. We can verify that $$710.88(1.08^{12})=1,790.11.$$

Further variations on annuities #

Annuities payable less frequently than once a year #

• Consider an annuity with regular payments of $200 payable at two yearly intervals in arrears.
• The final payment is made after 20 years.
• Find the PV at 6% per annum effective.

Method 1: Using First Principles

• Summing up the PVs of the individual payments, we get \begin{eqnarray*} \text{PV } &=&200\left( 1.06^{-2}+1.06^{-4}+\ldots +1.06^{-20}\right) \\ &=&200\times 1.06^{-2}\left(1+1.06^{-2}+1.06^{-4}+\cdots+1.06^{-18}\right)\\ &=&200\times 1.06^{-2}\frac{(1-1.06^{-20})}{1-1.06^{-2}}=\$1,\!113.58. \end{eqnarray*}

Method 2: Change the time unit

• New time unit is two-year
• The effective 2-year interest rate is \(j\) such that $$(1+j)=(1+i)^2=1.06^2\Longrightarrow j=12.36\%.$$
• The 2-year discount factor is \(v_i^2=1/(1+j)=v_j\).

Then the PV of this annuity is \begin{eqnarray*} 200\times a_{\angl{10}\,\,@j}=200\frac{1-v_i^{20}}{j}=200\frac{1-v_j^{10}}{j}=\$1,\!113.58. \end{eqnarray*}

Annuities with variable interest rate #

Consider the following \(m+n\) year annuity in arrears:

• If the effective annual interest rate is \(i\) throughout the term, then the PV of the annuity is \({a}_{\angl{n+m}\ i}\), and the accumulated value is \({s}_{\angl{n+m}\ i}.\)

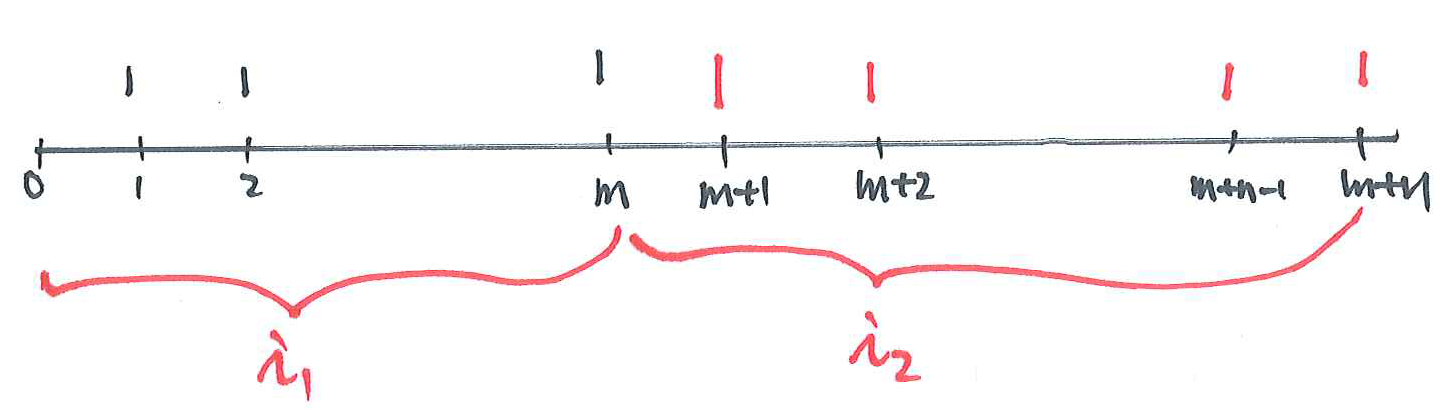
• If the interest rate is \(i_1\) by time \(m\) years, and the interest rate is \(i_2\) after time \(m\) years, then the PV of the annuity is $$a_{\angl{m}\ i_1}+v_{i_1}^m a_{\angl{n}\ i_2}$$

Annuities with variable payment amounts #

Consider the following annuity in arrears with term \(2n\) years with constant annual effective interest rate \(i\):

Define \(j=(1+i)^2-1\). The PV of this annuity is $$a_{\angl{2n}\ i}+a_{\angl{n}\ j}=(1+i) a_{\angl{n}\ j}+2a_{\angl{n}\ j}=\ldots$$

References #