Compound Interest #

Definition #

Compound interest differs from simple interest in that the investor can earn interest not only on the original investment (often called the principal) but also on interest paid in the past.

Consider an investment of $10,000 for a period of three years. Suppose that the interest rate offered is 6% per annum simple. The accumulated value of this investment after three years can easily be calculated: \begin{align*} A=P(1+r\,t)=10,000(1+0.06\times 3)=\$11,800. \end{align*} Here we assume that interest is not paid at the end of each year.

Under compound interest, interest is paid periodially. If it is paid annually, then we can see the increases in the principal as per the table below:

Note that the accumulated value of the initial $10,000 investment is greater under compound interest than under simple interest at the end of years 2 and 3. This is the effect of earning interest on interest (the compounding effect giving its name to compound interest!).

Example 1 #

Suppose that $10,000 is invested for a period of 10 years.

Suppose also that the compound interest rate offered is 7% per annum effective.

Find the accumulated value of this investment after

1. one year;

2. two years; and

3. ten years.

Solution to Example 1 #

1. After 1 year, the accumulation is $$$10,000(1+0.07)=$10,700. $$

2. After 2 years, the accumulation is

3. Similarly after 10 years, the accumulation is

General formula #

Given the following notation, write down a formula for \(A\) in terms of the other variables.

Notation:

• \(P\) = principal

• \(i\) = rate of compound interest per period

• \(n\) = term of investment (number of periods)

• \(A\) = accumulated value of original investment

We get

Remarks:

• Note that this formula also works for non-integer time periods \(n\).
• If any three of \(P, A, i, n\) are given, you are expected to know how to calculate the other one.
• If one period is one year, then \(i\) is the compound interest rate per annum.

Example 2 #

• Assume that compound interest is earned at the rate of 7% per annum effective (i.e. compounding annually).
• How much money do I need to invest today if I want to have $10,000 in ten years’ time?
• Let the investment today be \(P\). We require $$P(1.07)^{10} = 10,\!000$$ giving $$P = \frac{10,!000}{(1.07)^{10}}=$5,!083.49.$$
• Note here we have discounted $10,000 for 10 years.

Comparison of simple and compound interest #

Accumulated values #

An important result: \begin{eqnarray*} 1+i\,t&>&(1+i)^t, \quad \text{for}\,\, 0<t<1,\\ 1+i\,t&=&(1+i)^t, \quad \text{for}\,\, t=1,\\ 1+i\,t&<&(1+i)^t, \quad \text{for}\,\, t>1.\qquad\qquad\qquad\qquad\qquad\qquad \end{eqnarray*}

As an illustration, consider two cases:

• \(i=0.05\) and \(t=1/2\). Then
• \(i=0.05\) and \(t=2\). Then

In the short term (30% in red, 20% in black, 10% in blue) #

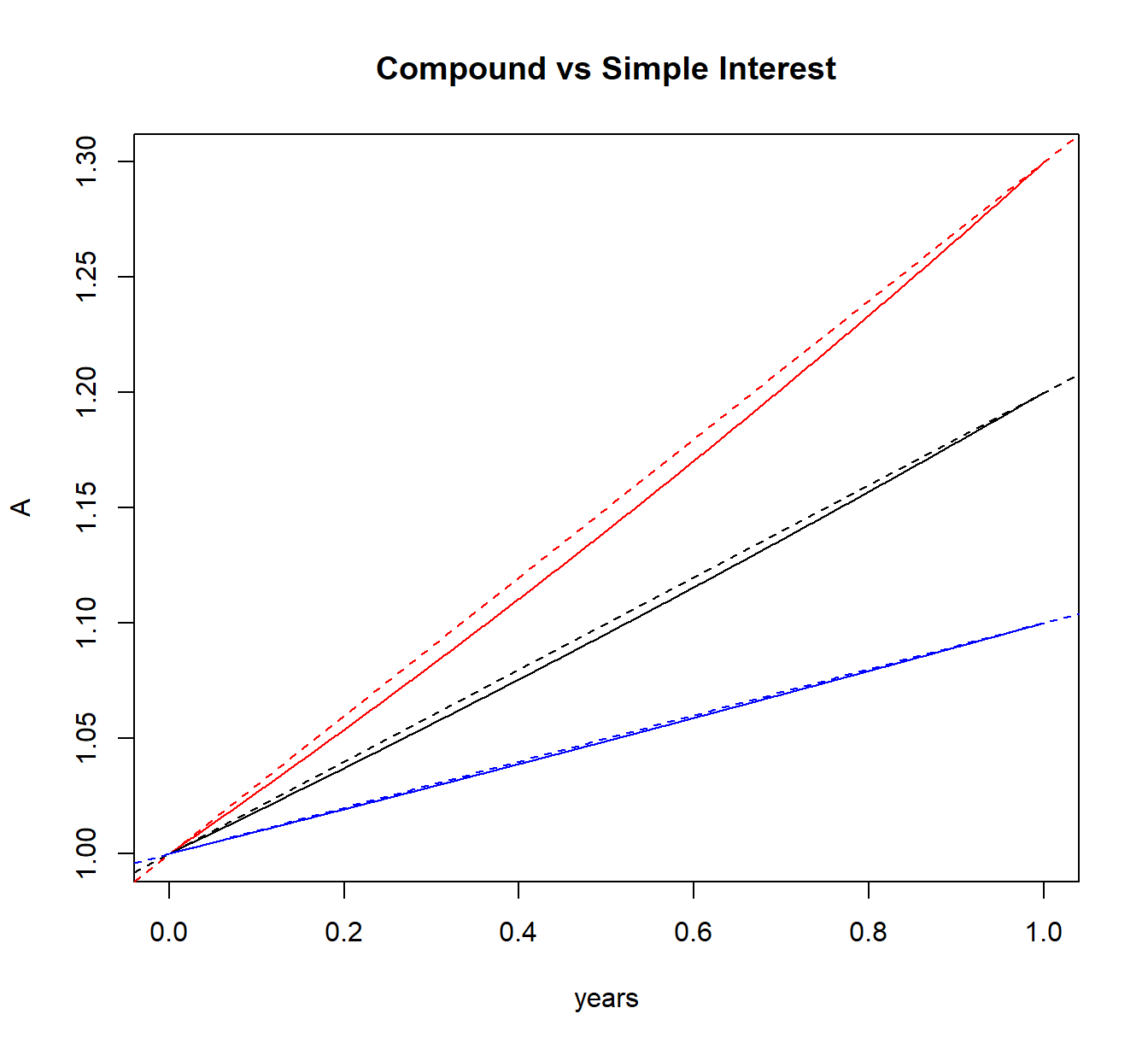
dashed: simple / solid: compound

In the long run (10% in red, 5% in black, 2% in blue) #

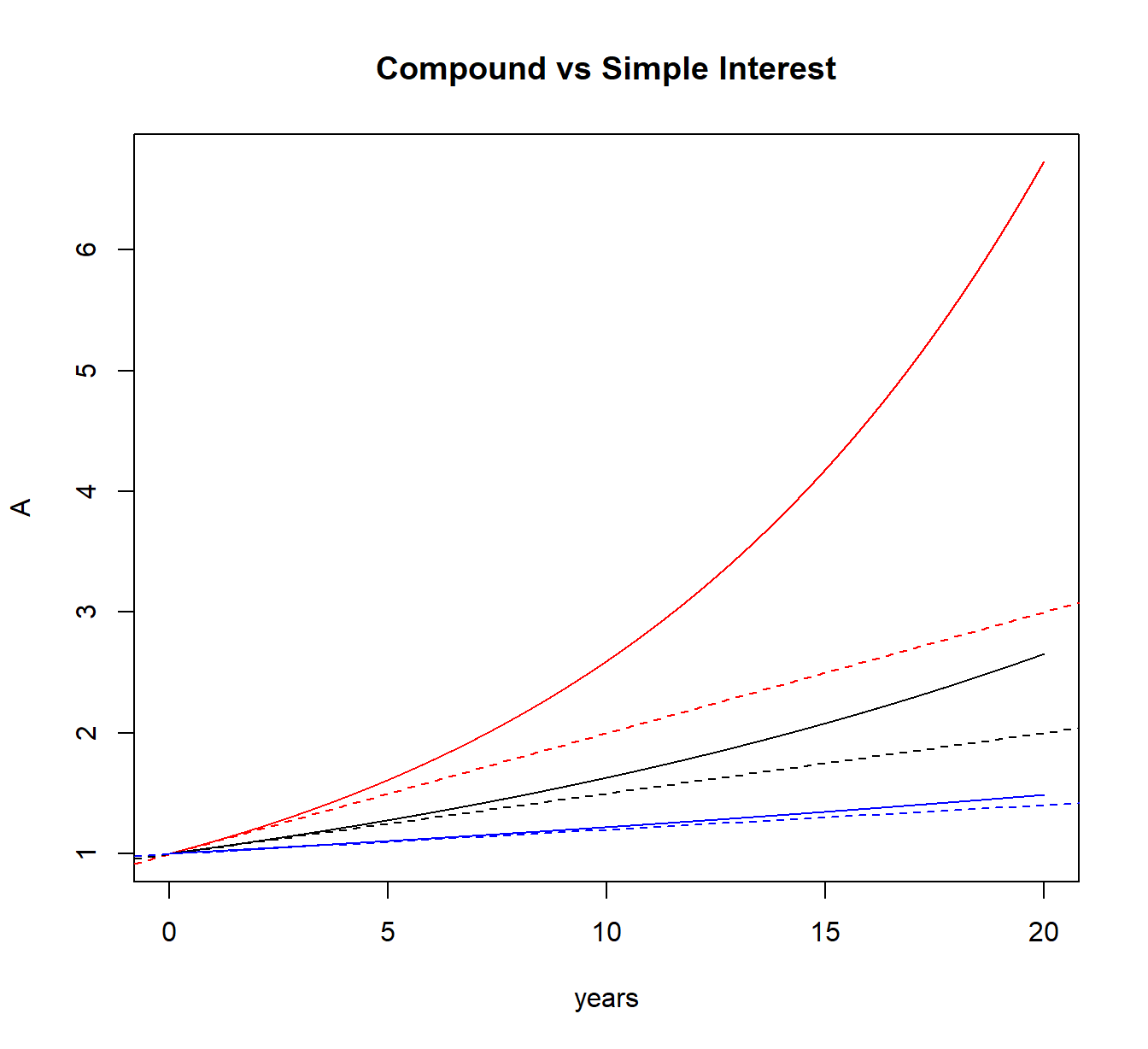
dashed: simple / solid: compound

Discounting #

Present Value and “Discounting” #

• “Discounting” is the inverse (opposite operation) of “Accumulating”
• The result is called a “Present value” (as opposed to an “Accumulated Value”)

More specifically:

• Consider an amount of money, \(A\), due in \(n\) years’ time.
• Suppose, as previously, that the rate of compound interest is \(i\) per annual effective.
• How much money needed now so that its accumulated value is \(A\)?
• This amount, denoted as \(P\), is called the present value (PV) of \(A\) dollars in \(n\) years’ time.
• When \(P\) is invested for \(n\) years at a compound rate of interest of \(i\) per annum effective, it will increase to exactly \(A\) dollars.

Using our compound interest accumulation result, we have giving Remarks:

• It follows therefore that we need to invest \(\ A(1+i)^{-n}\) today in order to have \(A\) dollars after \(n\) years.
• We say that $A(1+i)^{-n}$ is the (discounted) present value of \(A\) due in \(n\) years’ time.
• \(A\) is said to be the accumulated value of \(P\) at the end of \(n\) years.

Notation #

Define the discounting factor \(v\) as

• It should be clear to you that \(v\) is the present value of 1 due in one year’s time when compound interest is levied at rate \(i\) per annum effective.
• It should also be clear that the present value, \(P\), of \(A\) dollars due in \(n\) years’ time, assuming compound interest is levied at rate \(i\) per annum effective, can be written as
• We will make considerable use of the symbol \(v\) in actuarial studies and actuarial work.

Example 3 #

• Find the present value of $25,000 due in 15 years’ time.
• Assume compound interest at 5% per annum effective.
• The present value is then \begin{eqnarray*} && 25,000\,v^{15} \\ && =25,000\times1.05^{-15} \\ && =\$12,025.43. \end{eqnarray*}

Nominal and Effective Interest Rates #

Effective rates of interest #

The word “effective” has meaning:

• So far we have worked with annual effective rates of compound interest.
• The word “effective” is used when compounding is involved.
  It tells us that compounding occurs once per time period.
• This means that there will be rates that are not effective.
• In particular, “nominal” rates p.a. are are typically effective for a different time period than annual.

For example:

• Consider an investment of $10,000. Suppose that the compound rate of interest is 10% per annum. We consider two situations:
  • If compounding occurs only once in the year, then the accumulated value of the investment at the end of the year will be $$A=10,000\times 1.1=$11,!000.$$ Here we say that the interest rate is 10% per annum effective.
  • If instead compounding occurs twice in the year, then the accumulated value of the investment at the end of the year is calculated as $$ A=10,000\left( 1+\frac{1}{2}0.1\right) \left( 1+\frac{1}{2}0.1\right) =$11,025.$$ Here we say that the interest rate is 10% per annum convertible half-yearly.

Connecting effective and nominal rates with formulas #

Introductory example #

Let’s start with an example:

• What is the annual effective interest rate equivalent to an interest rate of 10% per annum convertible half-yearly?
• We can answer this question by noting that under an interest rate of 10% per annum convertible half-yearly, $10,000 grows to $11,025 at the end of the year. Hence we can solve for the unknown annual effective rate using $$11,025=10,000(1+i)$$ giving \(i=10.25\%\).

Note:

• It makes sense that the annual effective rate is higher than the equivalent compound interest rate convertible half-yearly.
• Notation: For the annual effective rate of interest, we have already seen that we write \(i=0.1025\). For the interest rate convertible half-yearly, we will write \(i^{(2)}=0.1\).

In general… #

We now define \(i^{(m)}\) as the nominal rate of interest convertible \(m\)-thly.

Note:

• \(m\) can take different values, such as \(m=2, 4, 12, 52, 365, 365\times 24.\)
• So for example, if interest compounds monthly, we will use the notation \(i^{(12)}\). We say that \(\frac{i^{(12)}}{12}\) is the monthly effective rate of compound interest earned.
• \(\frac{i^{(365)}}{365}\) is the daily effective rate of compound interest earned.

Generally speaking $$\frac{i^{(m)}}{m}$$ is the $1/m$-year effective rate of compound interest earned.

Accumulation and Discounting under nominal \(i^{(m)}\) #

Accumulation #

If the nominal rate of interest is \(i^{(m)}\) convertible \(m\)-thly, the accumulated value of principal \(P\) after \(n\) years (i.e. after \(mn\) compounding periods) is $$A=P\left( 1+\frac{i^{(m)}}{m}\right) ^{mn}.$$

Example 4 #

• Suppose that $5,000 is invested at a nominal rate of interest of 9% per annum convertible monthly.
• The accumulated value of this investment after 2.5 years is \begin{eqnarray*} && A=5,\!000 \left( 1+\frac{0.09}{12} \right) ^{12\% \times 2.5} \\ && =5,\!000 \times 1.0075^{30} \\ && =6,\!256.36. \end{eqnarray*}

Present Values and Discounting #

We can also find present values when the interest rate is expressed as a nominal rate convertible \(m\)-thly. By re-arranging the formula we get (Which is exactly the same idea as under effective rates.)

Example 5 #

• What sum of money, due at the end of 5 years, is equivalent to $1,800 due at the end of 12 years?

• Assume the nominal rate of interest is 11.75% per annum compounding half-yearly – that is, $$i^{(2)}=11.75\%.$$

• The question requires us to discount $1,800 for 7 years. We get \begin{eqnarray*} && A=1,\!800\left(1+\frac{0.1175}{2}\right)^{-2\% \times 7} \\ && =1,\!800\times 1.05875^{-14} \\ && =809.40. \end{eqnarray*}

Example 6 #

• A consumer buys goods worth $1,500. She pays $300 deposit and will pay $500 at the end of 6 months.
• If the store charges interest at \(i^{(12)}=18\%\) on the unpaid balance, what final payment will be necessary after one year?

Consider the following approach:

• Let the unknown payment be \(X\)
• Let the present value of all payments be $1,500, the purchase price of the goods.

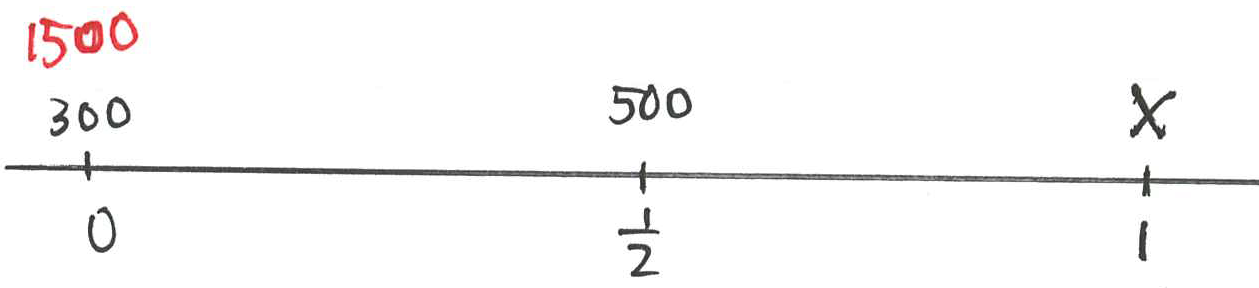
• Mathematically, we have $$1,500=300 + 500(1.015^{-6})+X(1.015^{-12})$$
• Solving this equation for \(X\), we get $$X=888.02.$$

The relationship betwen \(i\) and \(i^{(m)}\) #

Let

• \(i^{(m)}\) be the nominal rate of interest convertible \(m\)-thly, and let
• \(i\) be the effective rate of compound interest per annum.

Then we have \begin{eqnarray*} 1+i&=&\left( 1+\frac{i^{(m)}}{m}\right) ^{m},\\ \\ i^{(m)}&=&m\left\{ (1+i)^{1/m}-1\right\}\,. \end{eqnarray*}

The Force of Interest – Continuous Compounding #

Concept #

• You will note in the last the line of the above table we have nominal rates of interest with compounding occurring infinitely many times per year.
• This means that compounding must be occurring continuously.
• Continuous compounding has a very important role to play in theoretical actuarial and financial mathematics.
• The nominal rate of interest with continuous compounding is called the force of interest.

Notation: $$\lim_{m\rightarrow \infty }i^{(m)}=\delta.$$

Main formulas #

In fact, we have that the accumulation factor for \(\delta\) p.a. is $$ e^\delta = 1+i $$ if \(i\) is the equivalent effective rate of interest per annum. For \(t\) years this becomes $$ (1+i)^t = \left( e^{\delta} \right)^t = e^{\delta t}.$$

Example 7 #

1. Calculate the present value (PV) of $10,000 due in 6 years at a force of interest of 7% per annum.
2. Calculate the nominal rate of interest, convertible half-yearly, that is equivalent to a force of interest of 8% per annum.

We have:

1. \(10,\!000e^{-0.07\times 6}=6,\!570.47\)
2. Let the unknown nominal rate of interest be \(i^{(2)}\). Consider the accumulation of $1 under each form of interest.

\begin{eqnarray*} && e^{0.08}=(1+i^{(2)}/2)^2\\ &&\implies i^{(2)}=2(e^{0.04}-1)=0.0816. \end{eqnarray*}

Properties: \(i>\delta\) #

Mathematics Reminder: Taylor series expansion for \(e^{x}\) is so that $$e^\delta = 1+\delta+\frac{\delta^{2}}{2!}+\frac{\delta^{3}}{3!}+\ldots = 1+i$$ and hence $$i > \delta,$$ which makes sense, since \(i\) is compounded only once a year, and \(\delta\) continuously…

A proof #

Proof #

We have \begin{eqnarray*} \delta &=& \lim_{m\rightarrow \infty }i^{(m)} \\ &=& \lim_{m\rightarrow \infty }\hspace{0.2in}m\left\{ (1+i)^{1/m}-1\right\} \\ &=& \lim_{m\rightarrow \infty }\hspace{0.2in}m\left\{ e^{D/m}-1\right\} \qquad \text{where }D=\log (1+i) \\ &=& \lim_{m\rightarrow \infty }\hspace{0.2in}m\left\{ 1+\frac{D}{m}+\frac{% D^{2}}{2m^{2}}+\frac{D^{3}}{6m^{3}}+...-1\right\} \\ &=& \lim_{m\rightarrow \infty }\hspace{0.2in}\left\{ D+\frac{D^{2}}{2m}+\frac{% D^{3}}{6m^{2}}+...\right\} \\ &=& D \\ &=& \log (1+i) \end{eqnarray*} and hence $$ 1+i = e^\delta.$$

Varying Interest Rates #

Summary #

We have the following expressions for accumulating $1 for one year: \begin{align*} 1+i &=\left( 1+\frac{i^{(m)}}{m}\right) ^{m} \\ &=e^{\delta }. \end{align*} We also have the following expressions for discounting $1 for one year: \begin{align*} v &= \frac{1}{1+i} \\ &=\left( 1+\frac{i^{(m)}}{m}\right) ^{-m} \\ &=e^{-\delta }. \end{align*}

Equivalent Interest Rates #

• We have already seen that, for example, 10% per annum convertible quarterly is equivalent to 2.5% per quarter effective.
• This equivalence in interest rates means that we can calculate present values and accumulations of payments in different ways and get the same result.
• You must be able to move from one definition to another with ease.

Example 8 #

Find the PV of $10,000 due in 10 years’ time at 10% per annum convertible quarterly.

Solution

• Method One: Use the nominal rate of 10% and annual time period:
• Method Two: Use a time period of quarter years:

Example 9 #

• An insurer invests $50,000 at a nominal rate of 9% per annum convertible monthly.
• This investment has to provide payments in 3 years’ time and in 8 years’ time.
• If the payments are of equal amount, what is the amount of each payment?

Approach to Problem: Let the unknown payment be \(X\). Find the present value of the payments and equate this to $50,000. Measuring time in months, we get $$ 50,000=X(1.0075)^{-3\times 12}+X(1.0075)^{-8\times 12} =1.2522X$$ and hence $$X=39,929.38.$$ Suggestion: check your answer by following the progress of the fund
over the next 8 years in a spreadsheet.

Calculations with a mix of rates #

• We often hear in the media that the Reserve Bank of Australia is considering a change in the official level of interest rates.
• Such changes in official interest rates are generally reflected in the interest rates charged by lenders of funds and the interest rates offered to lenders of funds.
• In our studies we must therefore include methods for determining accumulations and present values when interest rates vary with time.
• We illustrate this in the following examples.

Example 10 #

• Suppose that the annual effective rate of compound interest is 8% per annum for 3 years and then 6% per annum effective for 5 years.
• The accumulated value after 8 years is

Example 11 #

• Suppose, as in the previous example, that the effective rate of interest is 8% per annum for 3 years and then 6% per annum for 5 years.
• Suppose that $100 is invested now and a further $100 is invested in 2 years’ time.
• The accumulated value after 8 years is

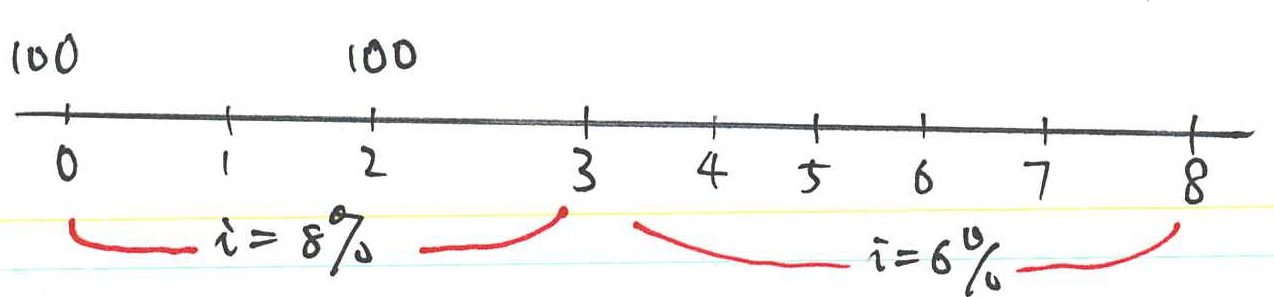
Example 12 #

Find the present value of $10,000 due in 10 years’ time, if

1. \(i^{(4)}=8\%\) for the first 3 years,
2. \(i^{(2)}=10\%\) for the next 5 years, and
3. \(i=9\%\) for the last 2 years.

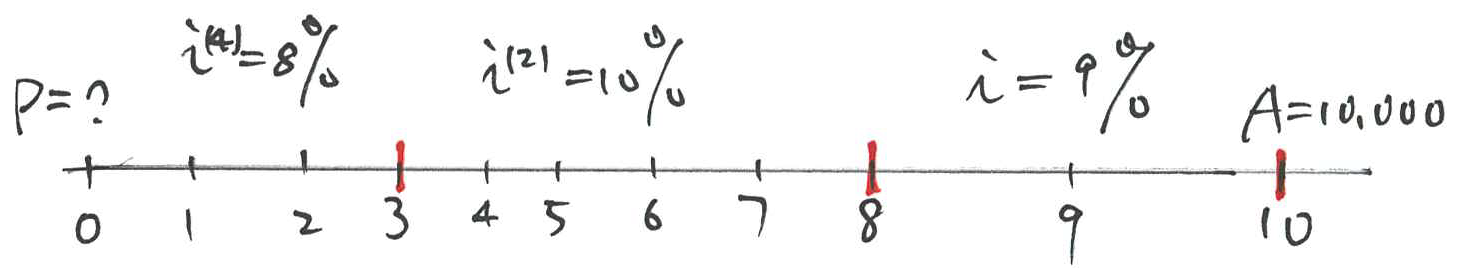
Draw a time line showing the payment and the interest rates. (This is a useful technique which can be applied to much more advanced problems.)

1. Step 1: Find the value in 8 years’ time:
2. Step 2: Find the value in 3 years’ time:
3. Step 3: Find the value now

When you are familiar with those calculations you should be able to write the solution directly as

Example 13 #

Bob invests $500 for 4 years. The nominal interest rate remains 8% each of the following 4 years, BUT:

• in the first year it is convertible half-yearly,
• in the second year it is convertible quarterly,
• in the third year it is convertible monthly and,
• in the fourth year it is convertible daily.

1. What is the accumulated value?
2. How much greater is this value than the corresponding value assuming that the first year rate had remained unchanged for the 4 years?

1. The accumulated value is
2. If the first year rate had remained unchanged for 4 years, our accumulation would have been The difference is just .

Describing Interest Rates Accurately #

It is important to describe interest rates in an unambiguous manner. For example:

1. 10% per annum simple interest.
2. 8% per annum simple discount.
3. 6% per annum effective.
4. 8% per annum convertible half-yearly.
5. 4% per half annum effective.
6. 5% per annum continuously compounded.
7. force of interest = 5% per annum.

References #