Time value of money #

• Interest corresponds to the time value of money
• It is a mathematical model to reflect the fact that most people would rather have a dollar now than in the future
• How much this time value of money is will depend on
  • How impatient you are
  • Any perceived risk

Simple Interest #

Interest Rates #

• Typically, interest is paid after a while (not continuously)
• Let us focus first on interest earnt in-between payment times
• This is what we call Simple interest
• This model is generally valid only for short term situations
• Most people are familiar with this, and we start by reviewing some examples

Examples #

Example #

Suppose John lends $10,000 to a bank.

Suppose that the bank agrees to pay simple interest at 12% per annum.

Suppose further that John will require repayment of his lent funds, along with the simple interest earned, in three months’ time.

How much money will John be paid at maturity, i.e. in three months’ time?

Solution to Example #

Given that we are operating with simple interest, John earns interest on his initial investment at the rate of 1% each month. The cash flow at the end of each month is

\begin{eqnarray*} \text{Interest}=10,000 \times 0.01 \times 3=300 \end{eqnarray*} His closing balance at the end month 3 is therefore equal to \begin{eqnarray*} \$10,000+\$300=\$10,300. \end{eqnarray*}

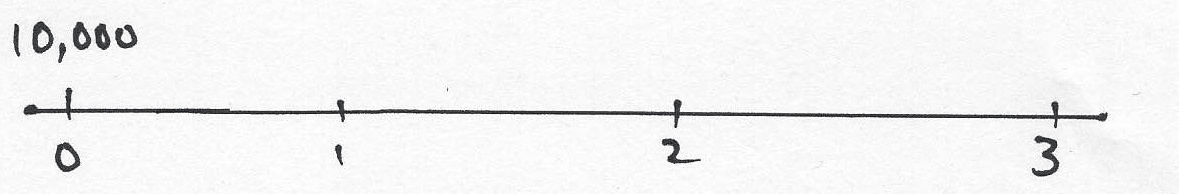
Example 1 #

• Given the following notation, write down formulae for \(I\) and \(A\) in terms of the other variables.
• Notation:
  • \(P\) = principal (i.e. the amount lent or invested)
  • \(r\) = rate of simple interest (per term)
  • \(t\) = number of terms of the investment
  • \(I\) = interest earned
  • \(A\) = accumulated value of original investment at the end of the term.

Solution to Example 1 #

• Following the example immediately before this exercise, we have `
• Therefore `
• Remarks:
  • \(t\) can be a positive integer or a positive real number.
  • If any three of \(A, P, r, t\) are given, the other one can be calculated.

Example 2 #

Suppose I want to be paid $10,000 in two and a half years’ time.

Interest is quoted as 8% per annum simple.

Find the amount that I need to invest today.

Solution to Example 2 #

• Rewrite the question using notation:
  • \(P\) = ?
  • \(r\) = 8% per annum simple
  • \(t\) = 2.5 years
  • \(A\) = $10,000
• From the general formula, we have `

Example 3 #

Suppose you invested $10,000 on 23 September 2019

Find the accumulated value on 29 November 2019 assuming 8% per annum simple interest applies.

Solution to Example 3 #

• Rewrite the question using notation:
  • \(A\) = ?
  • \(P\) = $10,000
  • \(r\) = 8% per annum simple
  • \(t\) = (7+31+29) days = 67 days = 67/365 years
• From the general formula, we have \begin{align*} A &=P(1+r t) \\ &=10,000\left(1+0.08 \times \frac{67}{365}\right) \\ &=10,146.85 \end{align*}

Applications #

Application of Simple Interest: Commercial Bills #

• Examples of commercial bills include bank accepted bills and treasury notes.
• These financial instruments require an amount to be paid at a specific time in the future. The date of this future payment is called the maturity date of the bill.
• The bill is sold at a date prior to the maturity date at a discount to the amount required to be paid at maturity. The amount of this discount is often calculated using simple interest.

Bank Accepted Bills #

Treasury Notes #

Application of Simple Interest: Commercial Bills #

• Consider a bank bill which will mature on 31 August this year.
• Suppose that the bill was purchased on 21 July this year.
• The maturity value (also called the face value) of the bill is $100,000.

Find the price paid for the bill on 21 July so that the holder of the bill earns 6% per annum simple interest.

To answer this question, we set up the following equation: \begin{align*} \text{Price }\times \left( 1+0.06\,\frac{41}{365}\right) =100,000\Longrightarrow \text{Price}=\$99,330.54 \end{align*}

Simple Discount #

Simple Discount #

We now turn our attention to simple discount. This is different to simple interest in one important way.

Under simple interest we have seen that the amount of interest is calculated by applying the simple interest rate to the amount of money present at the onset (i.e. beginning) of the investment period

Under simple discount, the amount of the discount is calculated by applying the simple discount rate to the amount of money present at the end of the investment period.

Examples #

Example 4 #

Consider again the bank bill from the previous example.

We have a face value of $100,000 due to be paid on 31 August (i.e. at the end of the investment period).

The bill is purchased on 21 July in the same year as the maturity date.

Find the price paid on 21 July for the bill so that the holder earns 6% per annum simple discount.

Solution to Example 4 #

• The amount of the discount is calculated by starting with the maturity value and applying a 6% discount to this value for a period of 41 days.
• The amount of the discount is therefore `
• The price of the bill is therefore `
• Remark: Under the simple interest \(r=6\%,\) the price is $99,330.54.

Example 5 #

• Given the following notation, write down formulae for \(D\) and \(A\) in terms of the other variables.
• Notation:
  • \(P\) = amount of original investment
  • \(d\) = rate of simple discount
  • \(t\) = term of investment
  • \(D\) = discount earned
  • \(A\) = accumulated value of original investment.

Solution to Example 5 #

• Following the example immediately before this exercise, we have `
• Similarly, we get \begin{align*} P &=A-D=A(1-d t) \\ \therefore \quad A &=\frac{P}{1-d t} \end{align*}

Simple Interest vs Simple Discount #

Explanation #

Difference between Simple Interest and Simple Discount #

• From the bank bill example it should be clear to you that a simple interest rate of 6% is NOT equivalent to a simple discount rate of 6%.
• The bank bill had a different price when it was priced to earn 6% per annum simple interest compared to when it was priced to earn 6% per annum simple discount.
• This can be made clear by considering an item in a shop for which the price is discounted and then subsequently marked up.
• Suppose a suit costs $1,000 ($A$). The price is reduced in a sale by 20%. This is like applying a simple discount rate of 20% per annum to the price over a one year period. The new price ($P$) is $800.

Difference between Simple Interest and Simple Discount #

• Suppose now that the discounted price, \(P\), is now increased by 20%. This is like applying a simple interest rate of 20% to the price of the suit for one year. The new price is $960.
• After application of simple discount and then simple interest both at 20% per annum for a one year period, we do NOT get back to the same starting position. The price does not return to $1,000.

The relationship between simple interest rate \(r\) and simple discount rates \(d\) #

Case 1: The investment term is one year ($t=1$)

Define the following notation and procedure:

• Initial investment of \(X\) dollars.
• Invest for one year at simple interest rate \(r\) per annum.
• Let \(Y\) denote the accumulated value of \(X\) after one year.
• Discount \(Y\) for one year at simple discount rate \(d\) per annum.

Find \(d\) in terms of \(r\) such that the discounted value of \(Y\) is exactly \(X\).

The relationship between \(r\) and \(d\) when \(t=1\) #

• From simple interest results, we have `

• Now, we require `

The relationship between \(r\) and \(d\) when \(t\not=1\) #

Case 2: The investment term is \(t\)-year

Define the following notation and procedure:

• Initial investment of \(X\) dollars.
• Invest for \(t\)-year at simple interest rate \(r\) per annum.
• Let \(Y\) denote the accumulated value of \(X\) after \(t\)-year.
• Discount \(Y\) for \(t\)-year at simple discount rate \(d\) per annum.

Find \(d\) in terms of \(r\) such that the discounted value of \(Y\) is exactly \(X\).

Derivation of the relationship between \(r\) and \(d\) if term is \(t \,(t\not=1)\) #

• If \(r\) is given
  `
• On the other hand, if \(d\) is given
  `
• Equating the two quantities gives the relationship
  \begin{align*} 1+r\,t=\frac{1}{1-d\, t} &\implies r=\frac{d}{1-dt}\\ &\implies d=\frac{r}{1+rt} \end{align*}

Exercises #

Example 6 #

Find the simple interest rate equivalent to a discount rate of 20%.

1. Assume a one-year investment.
2. Assume a three-month investment.

Solution to Example 6 #

1. Using the result above, we have: \begin{align*} r=\frac{d}{1-dt}=\frac{0.2}{1-0.2\times 1}=0.25 \end{align*} Importantly the simple discount rate is lower than the equivalent simple interest rate. We have already seen this in the suit example.
2. Again, using the result above, we have: \begin{align*} r=\frac{d}{1-dt}=\frac{0.2}{1-0.2\times 0.25}=0.21 \end{align*}

Example 7 #

On 7 May 2020 an investor purchased a $1,000 bill, maturing on 8 August 2020, at 6% per annum simple discount.

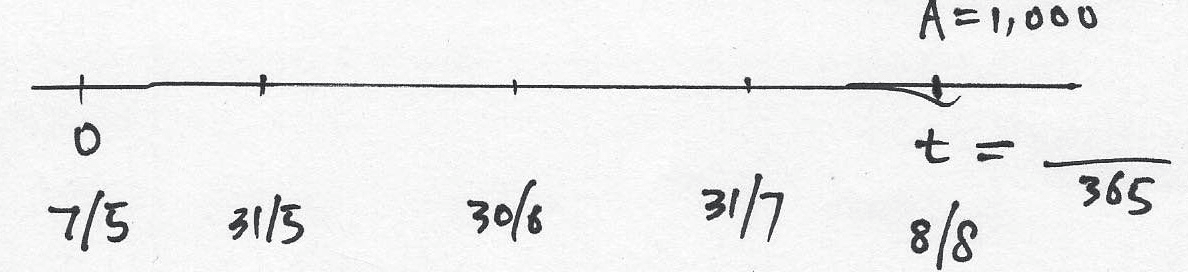
1. Calculate the price paid to the nearest cent.
2. What is the rate of simple interest per annum implied by this price? Give your answer to 4 decimal places.

Solution to Example 7 #

Number of days is \(24+30+31+8=93 \Rightarrow t=\frac{93}{365}\)

1. The price is given by `
2. The implied simple rate of interest is \begin{align*} r=\frac{d}{1-dt}=\frac{0.06}{1-0.06\times \frac{93}{365}}=0.0609 \end{align*}

References #